Some of the groups of contiguous notes relate to one another by 1. disregarding both the octave in which each note appears and when it appears relative to the others in the group, 2. placing each note of each group on a circle of half steps, forming a polygon, and 3. relating two polygons as either differing by a certain rotational distance or through a certain reflection.
For example, as shown below, the groups II and V have the same triangular shape, and one shape is a reflection of the other shape around an axis that falls between the notes B and C on the circle of half steps, shown with a dashed line. Music theorists call this relation inversion (I).
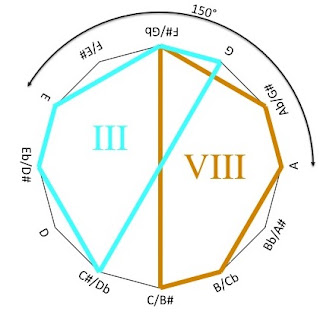
As another example, as shown below, the groups III and VIII have the same pentagonal shape, and one shape is, at minimum, a 150° rotation away from the other shape (allowing for either clockwise or counterclockwise rotation). When this rotation is directed, music theorists call this transposition (T).
This second example does not surprise, as the notes in group VIII are, in chronological order, all transposed down a perfect fifth from the notes in group III. The inversion of a perfect fifth is a perfect fourth, which is five-twelfths of an octave; likewise, 150° is five-twelfths of 360°.
However, as shown below, the same 150° rotational difference also relates the seven-note groups IX and X, each of which fill a full measure and have a similar single-line-then-big-chord presentation. This suggests a covert and distinctive employment of the perfect-fifth or perfect-fourth transposition, the most important transpositions in Western classical tonal music.
It stands to reason that a certain relation would be even more distinctive if it were a composite of both a certain rotational difference (one of six possible) and a reflection around a certain axis (one of twelve possible). One such composite relation occurs at least twice in this piece. As shown below, the five-note groups I and IV are related both by a 60° rotational difference and a reflection around the axis that falls on the note C, and so are the three-note groups VII and VIII.
I will leave it to the reader to find, and comment upon, two two-contiguous-note groups -- melodic intervals -- that are related by this same composite relation of 60° rotation and reflection around C. These two intervals also have the same articulation and same melodic-contour context.